How to Perform Multiplication of Exponents?

Exponents are an important part of algebra that forms the foundation of higher-level math studies like polynomial equations. Unfortunately, many students often struggle to understand and work with them. To master the vital skill of multiplying exponents it is important to go learn about the basics of exponents, their types, and rules so that it is convenient to apply them. Let’s begin with learning about exponents, their type, rules, and multiplication of exponents.

Exponents, Types & Rules

Exponents are the value that shows how many times a base number will multiply by itself. The number raised by power is known as the base, while the superscript number above it is the exponent or power.  Types of exponents are positive exponents, negative exponents, zero exponents, and rational exponents.

Positive exponents are simplified just by multiplying the base to itself the number of times indicated by the exponent/power. Negative exponents or the negative sign of an exponent means the reciprocal. You can simplify a negative exponent by using its fractional form where one represents its numerator and base with power represents the denominator. Zero exponents are expressions with the exponent as 0, and there is no need to consider the base value during simplification. Rational or fractional exponents will become radical or roots. For example, 31/3 can be written as 3root of 3, 65/2 can be written as two root (or square root) of 6 raises to the power 5. For learning exponent multiplications, it is important to know the 7 exponent rules. Let’s review them below:

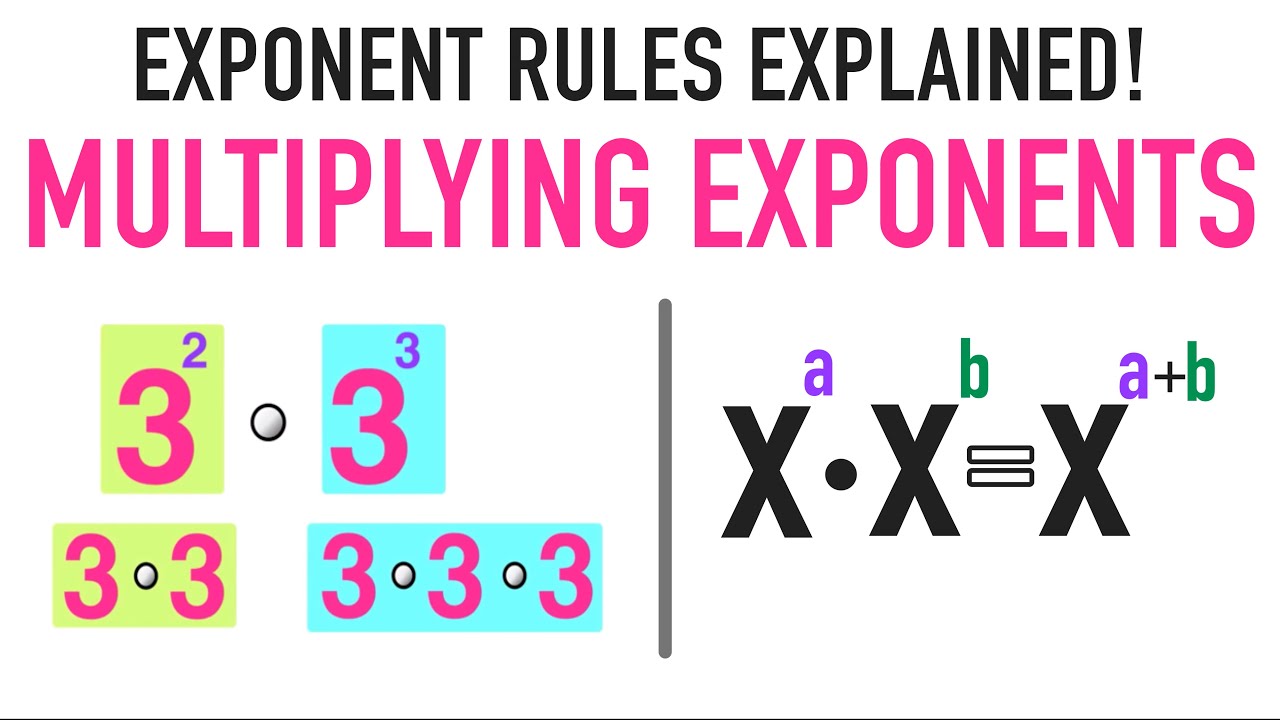
• Product of powers rule: When multiplying two bases of the same value, keep the bases the same and then add the exponents together to get the solution.
• The quotient of powers rules: Multiplication and division are opposites of each other, much the same, the quotient rule acts as the opposite of the product rule.
• Power of a power rule: This rule shows how to solve equations where power is being raised by another power. When dividing two bases of the same value, keep the base the same and subtract the exponent values.
• Power of a product rule: When any base is being multiplied by an exponent, distribute the exponent to each part of the base.
• Power of a quotient rule: A quotient simply means that you’re dividing two quantities. In this rule, you’re raising a quotient by a power. Like the power of a product rule, the exponent needs to be distributed to all values within the brackets it’s attached to.
• Zero power rule: Any base raised to the power of zero is equal to one.
• Negative exponent rule: When a number has a negative exponent, flip it into a reciprocal to turn the exponent into a positive exponent. Don’t use the negative exponent to turn the base into a negative.

4 Ways to Multiply Exponents

Here are four strategies that are simple shortcuts to simplify complicated equations. In order to find the actual value of an exponent, students must first understand what it means: repeated multiplication.

Multiplying Exponents with the Same Base

When you’re multiplying exponents, use the first rule: add powers together when multiplying like bases. For example, to find the product of 4^2 × 4^6, the bases of the equation stay the same, and the values of the exponents get added together.

That is, 4^2 × 4^6 = 4^8

Multiplying Exponents With Different Bases

It is possible to multiply exponents with different bases, but it requires the exponents to be the same. For example, to simplify  4^2 × 2^2 = ? first multiply the bases together and then, add the exponent. Instead of adding the two exponents together, keep it the same.

4^2 × 2^2 = 6^4 = 1296

Multiplying Exponents With Different Bases and Exponents

Multiplying different exponents with different bases is not possible. For example, 2^2 and 3^3 have nothing in common to combine, we can’t simplify them down into a single exponent and it should be expressed as a regular number.

Multiplying Negative Exponents

Multiplying exponents with negative powers may seem a little tricky but it is exactly the same as multiplying exponents with non-negative powers.

Learning about the properties of negative numbers will enable students to comfortably work with negative numbers before learning the multiplication of negative exponents. The main thing is to remember the exponent rule to change a negative exponent into a positive one by flipping it into a reciprocal. Then use the same above-mentioned ways to solve them.